viernes, 1 de noviembre de 2013
jueves, 31 de octubre de 2013
Cuerdas Vibrantes
QUE ES UNA CUERDA VIBRANTE?
Es un cable elastico, tendido entre 2 puntos fijos, suceptible
de emitir un sonido musicalgracias a sus vibraciones.Una tal cuerda , supuesta
cilindrica y homogenea, puede vibrar longitudinalmente otransversalmente es
alejada de su posicion de equilibrio. En musica utilizamosunicamente
vibraciones tranversales.Las cuerdas pueden ser hechas de acero (piano) o de
tripa de obeja; se les aumenta el peso envolviendolas en helice con un alambre
de cobre o de plata: obtenemos entoncescuerdas 'enfiladas' (notas graves del
piano, sol del violin; cuarta cuerda).
EXCITACION DE LA CUERDAPara alejar la cuerda de la posicion de
equilibrio podemos 'pelliscar' con el dedo (arpa),con una uña (guitarra) o con
una pluma o espina camandada por las teclas de un teclado(clavecin). La cuerda
puede ser golpeada por un martillo (piano) o incluso razgada por una rueda
(viela). Enfin, para el violin y los instrumentos del mismo tipo la cuerda
esatacada por un arco constituido por un gran numero de crines (de caballo) tendidos
eimpregnados de colofano para aumentar la aderencia a la cuerda.El arco empuja
la cuerda por frotamiento hasta el momento en el que la elasticidad de lacuerda
es mayor que el frotamiento: esta ultima vuelve a la posicion de equilibrio.
Elmismo fenomeno se reproduce un gran numero de veces por segundo y
encontramosque la frecuencia del fenomeno es la misma que la vibracion de la
cuerda, gracias alfenomeno de resonancia.
FORMULA DE LAS CUERDAS VIBRANTESUna cuerda fijada a sus 2
extremidades presenta siempre un nudo de vibracion en susextremidades y un
cierto numero de nudos intermediarios. Ese sistema de ondasestacionarias se
manifesta por un numero entero de zonas repartidas a lo largo de lacuerda. Si
vemos k zonas, la longitud de cada zona es λ/ 2 , la longitud total de lacuerda
L es dada por la expresion:
L = k *λ/ 2
γ siendo la frecuencia
y v la velocidad de ondas transversales. Obtenemos , puesto que
λ= v /γ
L = k * v / 2*γ
Pero
v=√(F /µ)d' où L = k /2γ
*√(F /µ)

Tubos Sonoros Cerrados y Abiertos
Un tubo cerrado con una longitud determinada sólo puede
producir una nota, la cual estará formada por una onda fundamental y unos
múltiplos de ésta, llamados armónicos. Estas ondas tienen que ser de tal forma
que en la zona de máxima compresión del aire del tubo (la parte cerrada) haya
un nodo y en la de mínima (la parte abierta), un vientre.
La longitud de un tubo es lo que determina que nota
escucharemos. Cuanto más largo es el tubo en cuestión más grave será la nota y
cuanto más corto, más aguda
Tubos sonoros
Se llaman tubos sonoros aquellos que contienen una columna
gaseosa (columna de aire) capaz de producir sonido al ser convenientemente
excitada. El cuerpo sonoro es la columna gaseosa, y no el tubo que la contiene;
en efecto, éste tiene la importante función de definir la forma de aquella pero
fuera de esto, influye relativamente poco sobre los fenómenos sonoros. Los
tubos sonoros pueden ser cerrados, es decir, que poseen una sola abertura y
tubos abiertos, que poseen dos o más.
Vibración de la columna de aire contenida en un tubo
Las columnas de aire contenidas en los tubos sonoros se
comportan, desde ciertos puntos de vista, como cuerdas musicales, por lo tanto
las columnas de aire vibrantes poseen nodos, o sea puntos donde la vibración es
nula, y vientres, equidistantes de los anteriores, donde la vibración alcanza
su máxima amplitud.
La vibración de las columnas de aire es longitudinal; los
nodos serán por tanto, puntos de condensación y los vientres puntos de
dilatación o rarefacción; en los extremos cerrados siempre se producen nodos y
en los extremos abiertos generalmente se producen vientres. El punto de
excitación no puede ser un nodo, pero no necesita ser un vientre, pudiendo
estar en un punto intermedio. No es necesario que las aberturas de un tubo
coincidan con los extremos, pudiendo éstos estar cerrados y haber una o más
aberturas en otras partes del tubo (la gaita).
Una columna de aire puede vibrar con toda su longitud o
dividida en segmentos iguales lo mismo que las cuerdas; en el primer caso se
obtiene el sonido llamado fundamental, y en los otros los armónicos: segundo,
si la columna vibra dividida en mitades; tercero, si vibra en tercios, etc.
Tomando como punto de partida el que en los extremos de un
tubo abierto, sólo pueden haber vientres de vibración, el tubo producirá su
fundamental cuando vibre con un nodo único en su centro. Cuando el tubo produce
su segundo armónico, producirá dos nodos y tres vientres; cuando produce su
tercer amónico, producirá tres nodos y 4 vientres, y así sucesivamente.
En los Tubos Cerrados, la onda se forma con un nodo en el
extremo cerrado y un vientre en el extremo abierto.
A igualdad de longitud de tubo, el tubo abierto produce un
sonido de frecuencia doble que el cerrado. Los tubos abiertos emiten la serie
completa de armónicos correspondientes a su longitud, mientras que los cerrados,
emiten sólo los armónicos de orden impar. Como tubo cerrado está la Flauta
Travesera y como tubos abiertos todos los demás: Clarinetes*, Oboes, Fagotes,
Saxofones, Trompetas, Trompas, etc.
Clasificación de los tubos sonoros
Los tubos sonoros se pueden clasificar de las siguientes
formas:
Según el modo de excitación de la columna de aire
Según la obtención de la escala
Según su forma interior
1.- Según el modo de excitación de la columna de aire pueden
ser: tubos de embocadura, tubos de lengüeta y tubos de lengüeta labial o
membranácea.
Tubos de embocadura son tubos sonoros que poseen una abertura
convenientemente dispuesta llamada embocadura, uno de cuyos bordes es biselado.
Contra este borde incide una corriente de aire que se divide en dos ramas; la
rama que penetra en el tubo origina pequeñas vibraciones que a su vez excitan
por resonancia la columna aérea contenida en el tubo. Estos se pueden dividir
en:
Tubos de embocadura directa. Los tubos de embocadura directa
son aquellos en que la corriente de aire es dirigida sobre la embocadura
directamente por los labios del ejecutante. La siguiente figura muestra una
embocadura de flauta travesera que es el prototipo de los instrumentos de
embocadura directa.

Efecto Doppler
El efecto Doppler, llamado así por el físico austríaco
Christian Andreas Doppler, es el aparente cambio de frecuencia de una onda
producida por el movimiento relativo de la fuente respecto a su observador.
Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der
Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz
en estrellas binarias y otros astros).
El científico neerlandés Christoph Hendrik Diederik Buys
Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y
confirmó que el tono de un sonido emitido por una fuente que se aproxima al
observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió
independientemente el mismo fenómeno en el caso de ondas electromagnéticas en
1848. En Francia este efecto se conoce como "efecto Doppler-Fizeau" y
en los Países Bajos como el "efecto Doppler-Gestirne".
En el caso del espectro visible de la radiación
electromagnética, si el objeto se aleja, su luz se desplaza a longitudes de
onda más largas, desplazándose hacia el rojo. Si el objeto se acerca, su luz
presenta una longitud de onda más corta, desplazándose hacia el azul. Esta
desviación hacia el rojo o el azul es muy leve incluso para velocidades
elevadas, como las velocidades relativas entre estrellas o entre galaxias, y el
ojo humano no puede captarlo, solamente medirlo indirectamente utilizando
instrumentos de precisión como espectrómetros. Si el objeto emisor se moviera a
fracciones significativas de la velocidad de la luz, sí sería apreciable de
forma directa la variación de longitud de onda.
Sin embargo hay ejemplos cotidianos de efecto Doppler en los que
la velocidad a la que se mueve el objeto que emite las ondas es comparable a la
velocidad de propagación de esas ondas. La velocidad de una ambulancia (50
km/h) puede parecer insignificante respecto a la velocidad del sonido al nivel
del mar (unos 1.235 km/h), sin embargo se trata de aproximadamente un 4% de la
velocidad del sonido, fracción suficientemente grande como para provocar que se
aprecie claramente el cambio del sonido de la sirena desde un tono más agudo a
uno más grave, justo en el momento en que el vehículo pasa al lado del
observador.

La moto (es la fuente sonora) emite un sonido, supongamos de
200 Hz de frecuencia, que viaja por el espacio hacia todas direcciones a una
velocidad de 343 metros por segundo. A su vez, la moto lleva una velocidad
propia, que supondremos de 80 km por hora (unos 22 m/s).
¿Qué sucede con los receptores respecto a la frecuencia con
que perciben el sonido de la moto?
Veamos:
Todo depende de las velocidades de los involucrados.
La chica de la izquierda está en reposo, respecto a ella, el
sonido debería llegar a la velocidad de 343 m/s, pero resulta que el emisor del
sonido (la moto) se aleja de ella a 22 m/s; por lo tanto, a ella le llega el
sonido solo a 321 m/s (343 menos 22), por lo tanto percibirá un sonido de menor
frecuencia (ondas más largas, tono menos agudo).
El muchacho de la derecha camina, supongamos a 3 m/s, hacia la
moto. Respecto a este muchacho, el sonido viaja hacia él a 343 m/s, más los 22
m/s de la moto y más los 3 m/s de su caminar hacia la moto; por lo tanto,
percibirá un sonido de mayor frecuencia, ondas más cortas, tono más agudo).
Entendida esta relación entre las velocidades, ahora
mostraremos cómo es posible obtener ecuaciones que nos permiten calcular las
variaciones de frecuencia percibidas por un receptor.
Para no complicar vuestra existencia estudiantil
estableceremos que la siguiente fórmula general permite hallar la frecuencia
que percibirá el receptor u observador:
Debemos fijar la atención en los signos + (más) y – (menos) de
la ecuación. Notemos que en el numerador
aparece como ± (más menos) y en el denominador aparece invertido (menos más).
Esta ubicación de signos es muy importante ya que usar uno u otro depende de si
el observador se acerca o se aleja de la fuente emisora de sonido.
Timbre
TIMBRE: Si se toca el situado sobre el do central en un
violín, un piano y un diapasón, con la misma intensidad en los tres casos, los
sonidos son idénticos en frecuencia y amplitud, pero muy diferentes en timbre.
De las tres fuentes, el diapasón es el que produce el tono más sencillo, que en
este caso está formado casi exclusivamente por vibraciones con frecuencias de
440 hz. Debido a las propiedades acústicas del oído y las propiedades de
resonancia de su membrana vibrante, es dudoso que un tono puro llegue al
mecanismo interno del oído sin sufrir cambios. La componente principal de la
nota producida por el piano o el violín también tiene una frecuencia de 440 hz.
Sin embargo, esas notas también contienen componentes con frecuencias que son
múltiplos exactos de 440 hz, los llamados tonos secundarios, como 880, 1.320 o
1.760 hz. Las intensidades concretas de esas otras componentes, los llamados
armónicos, determinan el timbre de la nota.

Tono
ALTURA O TONO: Cada sonido se caracteriza por su velocidad
específica de vibración, que impresiona de manera peculiar al sentido auditivo.
Esta propiedad recibe el nombre de tono.
Los sonidos de mayor o menor frecuencia se denominan
respectivamente, agudos o graves; términos relativos, ya que entre los tonos
diferentes un de ellos será siempre más agudo que el otro y a la inversa.
Intensidad
INTENSIDAD: La distancia a la que se puede oír un sonido depende de su intensidad, que es el flujo medio de energía por unidad de área perpendicular a la dirección de propagación. En el caso de ondas esféricas que se propagan desde una fuente puntual, la intensidad es inversamente proporcional al cuadrado de la distancia, suponiendo que no se produzca ninguna pérdida de energía debido a la viscosidad, la conducción térmica u otros efectos de absorción. Por ejemplo, en un medio perfectamente homogéneo, un sonido será nueve veces más intenso a una distancia de 100 metros que a una distancia de 300 metros. En la propagación real del sonido en la atmósfera, los cambios de propiedades físicas del aire como la temperatura, presión o humedad producen la amortiguación y dispersión de las ondas sonoras, por lo que generalmente la ley del inverso del cuadrado no se puede aplicar a las medidas directas de la intensidad del sonido.

Características del Sonido
Cualquier sonido
sencillo, como una nota musical, puede describirse en su totalidad
especificando tres características de su percepción: el tono, la intensidad y
el timbre. Estas características corresponden exactamente a tres
características físicas: la frecuencia, la amplitud y la composición armónica o
forma de onda.
Intensidad (Depende de la amplitud):
Distingue un sonido fuerte de uno débil.
Tono (Depende de la frecuencia):
Distingue a un sonido agudo (tono alto) de un sonido grave
(tono bajo).
Timbre (Depende de la forma de onda):
Distingue dos sonidos de la misma intensidad y tono, pero
producido por distintas fuentes.
Interferencia de una Onda Sonora
Se produce interferencia cuando varias ondas coinciden en un
mismo punto del medio por el que se propagan. Las vibraciones se superponen y
el estado de vibración resultante del punto es la suma de los producidos por
cada onda.
En las figuras adjuntas se representa la evolución de dos
estados de vibración transmitidos a un punto cuando es alcanzado por dos ondas
armónicas de la misma frecuencia. En el caso representado por el dibujo situado
más a la izquierda los estados de vibración (verde y rojo) llegan al punto en
fase y el resultado de su superposición es una vibración (azul) de mayor
intensidad. En ese punto tiene lugar una interferencia constructiva. En el otro
dibujo las vibraciones llegan en oposición de fase y el resultado de su
superposición es una vibración de menor intensidad (podría ser nula). Se
produce una interferencia destructiva.
La forma de producir interferencias consiste en hacer incidir
una onda sobre una pared con dos aberturas. Se produce difracción en cada una
de ellas y al otro lado de la pared se superponen las dos ondas secundarias
dando lugar a interferencias constructivas y destructivas.
Las líneas de color
continuas del esquema representan puntos en concordancia de fase con cada foco
(situado en una rendija) y las líneas discontinuas a puntos en oposición de
fase con él. A los puntos como B, C o D las ondas rojas (procedentes de F1)
llegan en fase con las ondas azules (procedentes de F2) mientras que a puntos
como el A, las ondas rojas llegan en oposición de fase con las azules. Así se
delimitan unas zonas donde se produce interferencia constructiva (se
representan por líneas negras de trazo continuo) y otras en las que se produce
interferencia destructiva (representadas
por líneas negras de trazo discontinuo).
Polarización de una Onda Sonora
La palabra polarizada proviene de polos, y alude a que los
polos (norte-sur; positivo-negativo; blanco-negro.
Es la vibración del campo electrico (o magnético) en una única
dirección.
En la onda,el campo eléctrico no tiene por qué estar siempre
vibrando en un plano.Ese plano puedo ir rotando (imagina una cuerda que hacen
vibrar dos personas,pero una de ellas en lugar de mover la mano siempre arriba
y abajo lo hace en un angulo variable) o estar fijo,o ser aleatorio,como ocurre
en la mayoría de las ondas a nuestro alrededor.
La polarización indica que el campo vibra en una unica
dirección.
1.Polarización lineal
si la diferencia es 0 o un múltiplo entero (positivo o
negativo) de Π.
2.Polarización circular
si la diferencia es un múltiplo entero (positivo o negativo)
3.polarización elíptica
En el resto de casos se producirá
4. Una onda no-polarizada se puede polarizar
Para polarizar una onda no-polarizada, basta con hacerla pasar
por una ranura, que, como no permite perturbaciones en más que una dirección,
transforma la onda en polarizada.
La ranura recibe el nombre de polarizador. Muchos
polarizadores de uso tecnológico son en realidad mallas de cientos y miles de
ranuras muy pequeñas y casi invisibles.
5.Una onda polarizada en una dirección puede polarizarse en
otra dirección.
Para cambiarle la dirección de polarización a una onda ya
polarizada, basta con hacerla pasar por un polarizador orientado en la nueva
dirección que se busca.
La onda resultante a la salida del polarizador posee una
amplitud menor que la onda incidente. La siguiente ecuación refleja el cambio:
A' = A cos θ, donde A' es la amplitud de la onda de polaridad modificada, A es
la amplitud de la onda original y θ es el ángulo de inclinación entre las
direcciones de polaridad.
Difracción de una Onda Sonora
La difracción es un fenómeno que afecta a la propagación del
sonido. Hablamos de difracción cuando el sonido en lugar de seguir en la
dirección normal, se dispersa en una continua dirección.
La explicación la encontramos en el Principio de Huygens que
establece que cualquier punto de un frente de ondas es susceptible de
convertirse en un nuevo foco emisor de ondas idénticas a la que lo originó. De
acuerdo con este principio, cuando la onda incide sobre una abertura o un
obstáculo que impide su propagación, todos los puntos de su plano se convierten
en fuentes secundarias de ondas, emitiendo nuevas ondas, denominadas ondas
difractadas.

La difracción se puede producir por dos motivos diferentes:
porque una onda sonora encuentra a su paso un pequeño
obstáculo y lo rodea. Las bajas frecuencias son más capaces de rodear los
obstáculos que las altas. Esto es posible porque las longitudes de onda en el
espectro audible están entre 1,7cm y 17m, por lo que son lo suficientemente
grandes para superar la mayor parte de los obstáculos que encuentran.
porque una onda sonora topa con un pequeño agujero y lo
atraviesa.
La cantidad de difracción estará dada en función del tamaño de
la propia abertura y de la longitud de onda.
Si una abertura es grande en comparación con la longitud de
onda, el efecto de la difracción es pequeño. La onda se propaga en líneas
rectas o rayos, como la luz.
Cuando el tamaño de la abertura es menor en comparación con la
longitud de onda, los efectos de la difracción son grandes y el sonido se comporta
como si fuese una luz que procede de una fuente puntual localizada en la
abertura.
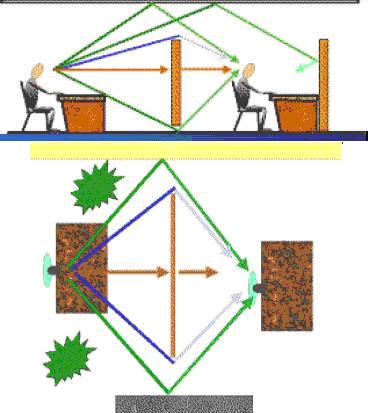
Refracción del Sonido
Refracción del Sonido
La refracción es la curvatura de
las ondas cuando entran en un medio donde su velocidad es diferente. La
refracción con el sonido no es un fenómeno tan importante como con la luz,
donde es responsable de la formación de imágenes por lentes, por el ojo,
cámaras, etc.
Sin embargo la curvatura de las ondas sonoras es una fenómeno
interesante en el sonido.
Si el aire por encima de la tierra es más caliente que en la
superficie, el sonido por refracción se dobla hacia atrás y hacia abajo en
dirección a la superficie.
El sonido desde una fuente puntual se propaga en todas las
direcciones. Normalmente, el oyente sólo puede oir lo que inicialmente se
dirigió hacia él, pero la refracción del sonido lo puede curvar hacia abajo.
Normalmente, sólo se recibe el sonido directo. Sin embargo, la refracción puede
añadir algo de sonido adicional, amplificando efectivamente el sonido. Sobre
lagos fríos, pueden darse lugar a amplificadores naturales.
Los pescadores tempraneros de la mañana, pueden ser las
personas más cercanas a la refracción del sonido. Considérese la posibilidad de
ir a un lago antes del amanecer. Justo cuando el sol se levanta sobre un lago
frío, se puede oír a alguien diciendo: "¡Buenos días!". Se mira
alrededor y no se ve a nadie. De todos modos, se está casi en el punto de
cuestionarse la cordura, siendo este momento de la mañana, se decide hacer caso
omiso. Pero la voz llega de nuevo, "Buenos días". Finalmente se
localiza al otro chiflado que se ha levantado a esta hora, al otro lado del
lago - mucho más allá de donde normalmente se oiría una voz-. Aquel pescador es
consciente del efecto del lago en la mañana temprano sobre la transmisión del
sonido. El agua fría mantiene frío el aire cercano, pero el sol de la mañana ha
comenzado a calentar el aire de más arriba, creando una "inversión
térmica". El hecho de que la velocidad del sonido sea más alta en el aire
mas caliente, curva algo del sonido hacia atrás en dirección a uno -sonido que
no llegaría al oído de uno en circunstancias normales-. Esta amplificación
natural sobre cuerpos frios de agua, es uno de los pocos ejemplos naturales de
la refracción del sonido.

Reflexión Una Onda Sonora
Reflexión se refiere al fenómeno por el cual una onda se
absorbe o regresa.
El tamaño del obstáculo y la longitud de onda determinan si
una onda rodea el obstáculo o se refleja en la dirección de la que provenía.
Si el obstáculo es pequeño en relación con la longitud de
onda, el sonido lo rodeara (difracción), en cambio, si sucede lo contrario, el
sonido se refleja (reflexión).
Si la onda se refleja, el ángulo de la onda reflejada es igual
al ángulo de la onda incidente, de modo que si una onda sonora incide
perpendicularmente sobre la superficie reflejante, vuelve sobre sí misma.
La reflexión no actúa igual sobre las altas frecuencias que
sobre las bajas. La longitud de onda de las bajas frecuencias es muy grande (pueden
alcanzar los 18 metros), por lo que son capaces de rodear la mayoría de
obstáculos; en cambio las altas frecuencias no rodean los obstáculos por lo que
se producen sombras detrás de ellos y rebotes en su parte delantera.

Ecuación de Onda
donde v es la velocidad de fase de la onda e y rde la onda. Esta es la ecuaciepresenta la variable que cambia al paso ón de onda que
aplica a una cuerda estirada o a una onda electromagnética plana. La descripción
matemática de una onda, hace uso de las derivadas parciales.
En dos dimensiones, la ecuación de onda
toma la forma
la cual podría describir una onda sobre membrana estirada.
Las Ondas Sonoras
Una onda sonora es una onda longitudinal que transmite lo que
se asocia con sonido. Si se propaga en un medio elástico y continuo genera una
variación local de presión o densidad, que se transmite en forma de onda
esferica periódica o cuasiperiodica. Mecánicamente las ondas sonoras son un
tipo de onda elástica.
Las variaciones de presión, humedad o temperatura del medio,
producen el desplazamiento de las moléculas que lo forman. Cada molécula
transmite la vibración a las que se encuentren en su vecindad, provocando un
movimiento en cadena. Esa propagación del movimiento de las moléculas del
medio, producen en el oído humano una sensación descrita como sonido.

Las Ondas Mecanicas
Una onda mecánica es una perturbación de las propiedades
mecánicas de un medio material (posición, velocidad y energía de sus átomos o
moléculas) que se propaga en el medio.
Todas las ondas mecánicas requieren:
1. Alguna fuente que
cree la perturbación.
2. Un medio en el que
se propague la perturbación.
3. Algún medio físico
a través del cual elementos del medio puedan influir uno al otro.
El sonido es el ejemplo más conocido de onda mecánica, que en
los fluidos se propaga como onda longitudinal de presión. Los terremotos, sin
embargo, se modelizan como ondas elásticas que se propagan por el terreno. Por
otra parte, las ondas electromagneticas no
son ondas mecánicas, pues no requieren un material para propagarse, ya
que no consisten en la alteración de las propiedades mecánicas de la materia
(aunque puedan alterarlas en determinadas circunstancias) y pueden propagarse
por el espacio libre (sin materia).

Ondas Longitudinales
Longitudinales: Una onda longitudinal es una onda en la que el
movimiento de oscilación de las partículas del medio es paralelo a la dirección
de propagación de la onda. Las ondas longitudinales reciben también el nombre
de ondas de presión u ondas de compresión. Algunos ejemplos de ondas
longitudinales son el sonido y las ondas sísmicas de tipo P generadas en un
terremoto.
Aquí podemos ver estas
y otras ondas
Frecuencia
Explicación de frecuencia
Las ondas periódicas son aquellas que tienen amplitudes
(altura de arriba a abajo) y longitudes de onda (la distancia entre las partes
superiores de las ondas) constantes. El período de una onda es el tiempo que
toma para realizar un ciclo completo. La frecuencia puede ser medida en una
variedad de unidades, pero las unidades estándar, como se determina bajo el
Sistema Internacional de Unidades, es un Hz. Un Hertzio (llamado así por el
físico Heinrich Hertz) representa una unidad de frecuencia. La frecuencia
también está representada por la letra f. El período es representado por la
letra T, y tiene una relación inversa con la frecuencia, de manera que T = 1 /
f. La frecuencia es también inversamente proporcional a la longitud de onda,
que está representada por el símbolo griego lambda.
Ondas de sonido y frecuencia
Todas las ondas de sonido tienen una frecuencia y ésta
determina el tono del sonido. El tono de un sonido es, en pocas palabras, qué
tan alto o bajo es, según lo reconoce el oído humano. Los sonidos agudos tienen
una frecuencia más alta, los graves tienen una frecuencia más baja. El tono,
sin embargo, no es un concepto científico. Las ondas sonoras no tienen ningún
tono, sino que simplemente oscilan más rápido o más lento y nuestros oídos
registran esta calidad como alta y baja. Las frecuencias de las ondas de sonido
se miden en Hertzios, como se describió anteriormente.
Ondas lumínicas y frecuencia.
El espectro de luz visible también cuenta con determinada
frecuencia. La luz visible se compone de rayos de campos eléctricos y
magnéticos oscilantes a través del espacio (o aire). Estos rayos son captados
por nuestros ojos y nuestro cerebro interpreta lo como color. Es la frecuencia
de estas ondas la que determina sus colores. Todos los colores se encuentran
entre 400 trillones de Hertzios (luz roja) y 800 trillones de Hertzios (luz
violeta).
Frecuencia en otras ondas
Todos los tipos de radiación electromagnética tienen una
frecuencia medible; sólo la frecuencia de estas ondas es o bien tan baja o tan
alta que son invisibles para el ojo humano sin ayuda. Las ondas de radio, las
microondas y las ondas de radiación infrarroja tienen una menor frecuencia que
la luz visible, las ondas de radio son las más bajas. Los rayos gamma, los
rayos X y los rayos ultravioletas tienen frecuencias que son mucho mayores que
la luz visible; los rayos gamma son los más altos.
Suscribirse a:
Entradas (Atom)

